De kapitein van het schip verwelkomt u aan boord voor een tripje over de woelige baren. U denkt: woelige baren? Maar die kan ik toch met wat goniometrische functies beschrijven?
Vraagstelling
De eeuwige vraag blijft welke koers (hoek ten opzichte van de wind) men moet varen om zo snel mogelijk naar een bovenwindse koers te geraken.
Oplossing
We bekijken het polaire diagram van een schip. Bij elke hoek van het schip ten opzichte van de ware wind komt een theoretische snelheid overeen. Het is logisch dat een hoek van 0° geen voorwaartse snelheid creëert. Naarmate de hoek groter wordt genereert men meer snelheid. Een straffe bries doet de zeilen bollen. U ziet onmiddellijk het verband tussen de zeilkoers en de ontwikkelde snelheid van het schip.
Stap 1:
We kunnen snelheidsfunctie van het zeiljacht met bijhorende koersen weergeven in een tabel. De functie met voorschrift f(x)=2x² {0.7<x} beschrijft de snelheid onder diverse hoeken in radialen ten opzichte van een ware windsnelheid van 7 knopen.
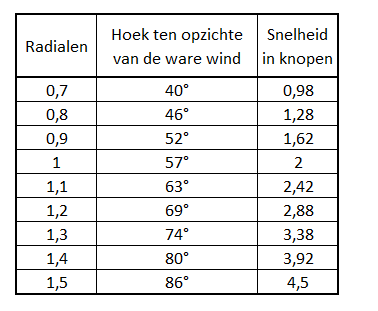
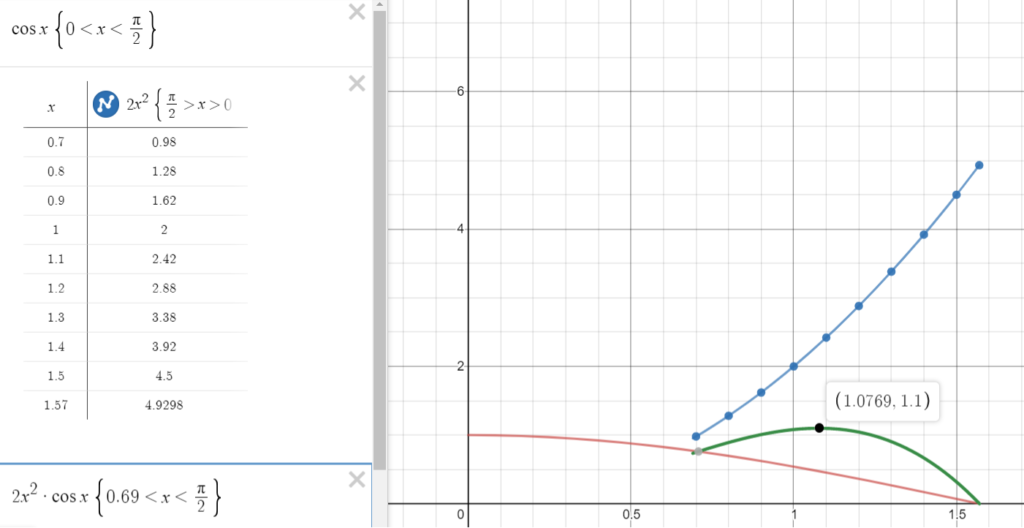
Stap 2:
We bekijken de ware snelheid naar de bovenwindse boei (de snelste koers naar de boei). Daarbij maken we gebruik van de cosinusregel. We vermenigvuldigen hierbij onze snelheidsfunctie f(x)=2x² met de cosinusfunctie g(x)=cos(x). We krijgen de functie o(x)=2x².cos(x). Deze functie heeft een maximum in het punt (1.0769;1.1). Aangezien de x-as in radialen uitgedrukt staat, geeft ons dat een hoek van 62° ten opzichte van de ware wind.
Het is logisch dat we sneller varen als de hoek van de ware wind groter wordt, maar dat impliceert ook dat we een grotere hoek varen ten opzichte van onze bestemming en dus meer afstand afleggen. Deze functie berekent ons het optimum, met andere woorden de optimale koers om zo snel mogelijk ons doel te bereiken.
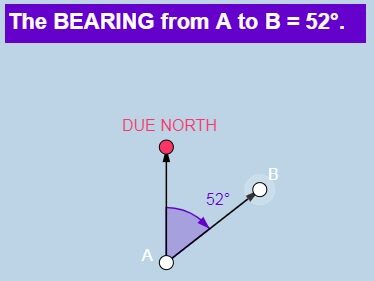
Controle
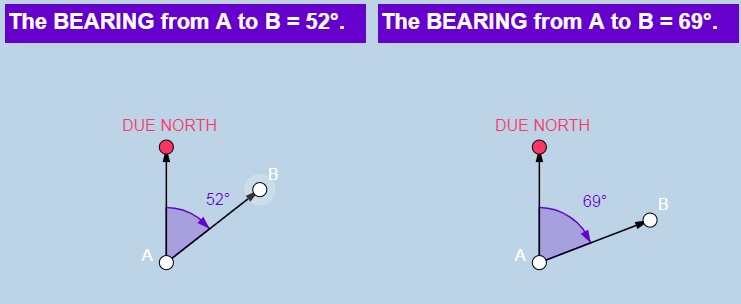
We veronderstellen twee zeilboten. Zeilboot A vaart een koers (=bearing) van 52° ten opzichte van de wind, terwijl zeilboot B een koers (=bearing) vaart van 69° ten opzichte van de wind. De rode boei ligt pal in de wind op een afstand van 5 nautische mijl (Nm).Met de cosinusregel rekenen we uit dat zeilboot A (2.5/cos(52°)*2) een afstand aflegt van 8,12 Nm, terwijl zeilboot B (2.5/cos(69°)*2) een afstand aflegt van 13,95 Nm. Toch zal zeilboot B sneller aankomen bij de bovenwindse boei. Delen we afstanden door de respectievelijke snelheden waaronder deze zeilboten varen dan zien we zeilboot A (8,12 Nm / 1.62 kn) 5 uur nodig heeft terwijl zeilboot B (13,95 Nm /2,88) ‘slechts’ 4,84 uur nodig heeft.Een te scherpe koers is dus niet altijd voordelig.De snelste koers wordt aangeven door ons optimum van de functie o(x)=2x².cos(x). Een koers van 62° is optimaal. Berekenen we de tijdsduur (2.5/cos(69°)*2) Nm / 2.42 kn dan bekomen we 4,4 uur.